Električna impedanca: definicija, reaktanca in vpliv frekvence
Električna impedanca: jasna definicija, reaktanca in vpliv frekvence. Formule, primeri in praktične razlage za induktorje, kondenzatorje ter praktične aplikacije.
Električna impedanca je mera upora, ki ga neko električno vezje predstavlja spremembam toka ali napetosti. Impedanca upošteva tako izgube v obliki upora kot tudi fazni zamik med napetostjo in tokom, ki ga povzročata reaktanci induktorjev in kondenzatorjev.
Predstavi impedanco: kompleksna in polarna oblika
Impedanco lahko zapišemo na dva glavna načina: (glej 2. sliko, "kompleksna ravnina impedance")
- z upornostjo "R" (realni del) in reaktanco "X" (imaginarni del), na primer Z = 1 + 1 j {\displaystyle Z=1+1j}
- z magnitudo in fazo (velikost | Z | {\displaystyle \left\vert Z\right\vert }
in kot ∠ θ {\displaystyle \angle \theta } 
), na primer Z = 1,4 ∠ 45 ∘ {\displaystyle Z=1,4\angle 45^{\circ }} 
(1,4 ohma pri 45 stopinjah)
V kompleksni obliki velja Z = R + jX, kjer je R realni del (upornost) in X imaginarni del (reaktanca). Magnituda in faza sta povezani z realnim in imaginarni delom preko formul:
- |Z| = sqrt(R² + X²) — velikost impedance.
- θ = arctan(X / R) — fazni kot (pozitivna X pomeni, da tok zaostaja za napetostjo pri induktivnem obnašanju; negativna X pomeni, da tok prednjači pri kapacitivnem obnašanju).
Impedanca v primerjavi z uporom
Impedanca in upor sta si v nekaterih pogledih podobna: višja vrednost pomeni večjo napetost potrebno za isti tok. Pri čisto upornem elementu (ohmskem uporu) velja Ohmov zakon:
V = R ∗ I {\displaystyle V=R*I}
, kjer je V napetost, R upornost in I tok.
Pri splošni impedanci se razmerje med amplitudo napetosti in toka opisuje z vezavo:
V = Z ∗ I {\displaystyle V=Z*I}
, kjer je Z kompleksna impedanca.
Reaktanca in vpliv frekvence
Glavna razlika med upornostjo in impedanco je v besedi "sprememba": impedanca je pogosto odvisna od hitrosti spremembe napetosti oziroma toka, kar običajno izražamo kot frekvenca (število nihajev na sekundo). V sinusnem stacionarnem stanju uvajamo kot pogostokrat uporabo kotne frekvence ω = 2πf.
Za idealen induktor velja:
Za induktor: Z = j 2 π f L {\displaystyle Z=j2\pi fL\,} 
Kjer je reaktanca induktorja X_L = ωL = 2πfL in je proporcionalna frekvenci. Pri višjih frekvencah induktor bolj upira toku (večji X_L).
Za idealen kondenzator velja:
Za kondenzator: Z = 1 j 2 π f C {\displaystyle Z={\frac {1}{j2\pi fC}}} 
Kjer je reaktanca kondenzatorja X_C = -1/(ωC) = -1/(2πfC). Pri višjih frekvencah je |X_C| manjša, zato kondenzator lažje prepušča hitro spreminjajoče komponente signala.
Posebni primeri frekvence:
- Pri f = 0 (stalan enosmerni tok) je impedanca induktorja približno 0 (kratki stik), ker DC povzročajo stalni tok skozi induktor.
- Pri f = 0 je impedanca kondenzatorja praktično neskončna (odprt krog), ker kondenzator ne more sproti napajati stalnega toka brez spremembe napetosti.
Fizikalni vidiki in energija
Na fizični ravni lahko poenostavimo:
- upor je posledica trkov elektronov z atomi v notranjosti upora — energija se razprši kot toplota;
- impedanco v kondenzatorju povzroči nastanek električnega polja, ki v njem shranjuje energijo (E = 1/2 C V²);
- impedanco v induktorju povzroči ustvarjanje magnetnega polja, ki v njem shranjuje energijo (E = 1/2 L I²).
Pomembna razlika: upor razpršuje (porablja) energijo, medtem ko induktor in kondenzator energijo shranjujeta in jo lahko vrneta nazaj v vezje, ko se pogoj spremeni. To ima neposredne posledice pri izmeničnih signalih in pri upravljanju reaktivne moči v napajanju.
Odboji, ujemanje in valovna impedanca
Če impedanci vira, kabla in bremena niso usklajene, se del signala odbije nazaj proti viru, kar povzroča odboj, izgubo energije in interference. Koeficient odboja izračunamo z naslednjo enačbo:
Γ = Z L - Z S Z L + Z S {\displaystyle \Gamma ={Z_{L}-Z_{S} \over Z_{L}+Z_{S}}}}
kjer Γ {\displaystyle \Gamma } 
(capital gamma) je koeficient odbojnosti, Z S {\displaystyle Z_{S}}
je impedanca vira, Z L {\displaystyle Z_{L}}
je impedanca bremena.
Za minimalne izgube in maksimalni prenos moči v prenosnih linijah običajno ujemamo impedanco vira s karakteristično (valovno) impedanco kabla in z bremenom (npr. 50 Ω ali 75 Ω pri RF sistemih). Prav tako velja pravilo kompleksnega konjugata za maksimalni prenos moči: učinkovit prenos nastane, ko je impedanca bremena konjugirana impedanci vira (Z_L = Z_S*).
Vsak medij, po katerem se prenaša valovanje, ima svojo valovno impedanco. Tudi prazen prostor, kjer se širi elektromagnetno valovanje (svetloba), ima valovno impedanco približno 377 Ω {\displaystyle \Omega } 
.
Praktični primer izračuna
Če imamo komponento z R = 1 Ω in X = 1 Ω, je kompleksna impedanca Z = 1 + j1. Njena velikost je |Z| = sqrt(1² + 1²) = sqrt(2) ≈ 1,414 Ω in fazni kot θ = arctan(1/1) = 45°. To ustreza zapisu Z = 1,4 ∠ 45 ∘ .
Zaključek
Impedanca je temeljna lastnost pri analizi vezij za izmenični tok in frekvenčno odvisnih sistemov. Razumevanje njene kompleksne narave, vpliva frekvence na reaktance ter pomena ujemanja impedanc omogoča pravilno načrtovanje elektronskih naprav, prenosnih linij in RF sistemov. Večinoma se pri nelinearnih ali časovno spremenljivih signalih uporabi razčlenitev signala na sinusoide (npr. preko Fourierjeve transformacije), saj vsaka frekvenčna komponenta doživlja svojo impedanco.
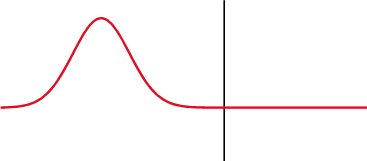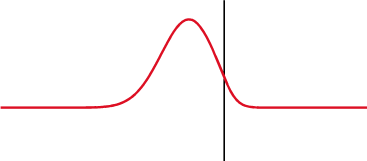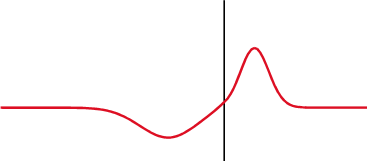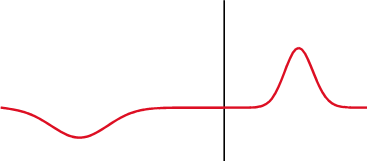
Signal se delno odbije nazaj, kjer se spremeni impedanca.
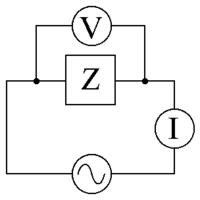
Napajanje z izmeničnim tokom z napetostjo V {\displaystyle \scriptstyle V} 
preko impedance Z {\displaystyle \scriptstyle Z}. 
, ki poganja tok I {\displaystyle \scriptstyle I}
.
Grafični prikaz ravnine kompleksne impedance
Faza
Na uporu se napetost in tok hkrati povečujeta in zmanjšujeta, zato pravimo, da sta v fazi, pri impedanci pa je drugače, napetost je za 1/4 valovne dolžine premaknjena za tok v kondenzatorju in naprej v induktorju.
1/4 valovne dolžine se običajno predstavlja z imaginarnim številom "j", ki je prav tako enakovredno 90-stopinjskemu premiku.
Zaradi uporabe imaginarnega števila "j" je matematika veliko preprostejša, saj omogoča izračun celotne impedance na enak način, kot to počnemo pri uporih, na primer upor in impedanca zaporedno je R+Z, vzporedno pa (R*Z)/(R+Z).
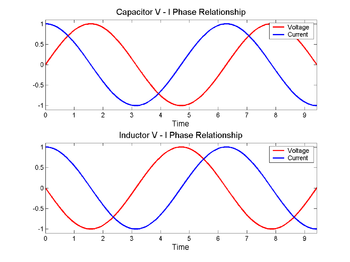
Na kondenzatorju (zgoraj) se napetost (rdeča) spremeni za tokom (modra), na induktorju (spodaj) pa prej. Fazna razlika med napetostjo in tokom je 1/4 valovne dolžine.
Vprašanja in odgovori
V: Kaj je električna impedanca?
O: Električna impedanca je nasprotje, ki ga vezje predstavlja za spremembo toka ali napetosti.
V: Kako lahko zapišemo električno impedanco?
O: Električno impedanco lahko zapišemo z upornostjo "R" (realni del) in reaktanco "X" (imaginarni del), pa tudi z velikostjo, fazo, velikostjo in kotom.
V: Kakšna je razlika med upornostjo in impedanco?
O: Ključna razlika med upornostjo in impedanco je v besedi "sprememba"; z drugimi besedami, hitrost spremembe vpliva na impedanco. Upor se upira vsakemu toku, ki teče skozi njega, medtem ko se induktor upira spremembam toka, kondenzator pa spremembam napetosti.
V: Katere formule so povezane z upornostjo in impedanco?
O: Za upornost velja V=R*I, kjer je V napetost, R upornost in I tok; za induktorje Z=j2πfL; za kondenzatorje Z=1/j2πfC; kjer Z predstavlja impedanco, j imaginarno število -1 , π konstanto pi, f frekvenco, L induktivnost in C kapacitivnost.
V: Katere so fizikalne razlage za upornost v primerjavi z impedanco?
O: Upor je posledica trkov elektronov z atomi v uporih, medtem ko je impedanca induktorja posledica ustvarjanja električnega polja, impedanca kondenzatorja pa posledica ustvarjanja magnetnega polja. Poleg tega upori razpršijo energijo, medtem ko induktorji in kondenzatorji shranjujejo energijo, ki se lahko vrne v vir, ko se zmanjša.
V: Kako izračunate koeficient odboja?
O: Koeficient odbojnosti lahko izračunamo z uporabo Γ=(ZL-ZS)/(ZL+ZS), kjer Γ (velika gama) pomeni koeficient odbojnosti; ZS pomeni impedanco vira; ZL pomeni impedanco bremena
Iskati