Vennov diagram: definicija, uporaba in zgodovina logičnih množic

Vennov diagram: jasna definicija, praktične uporabe in zgodovina logičnih množic — razumite preseke, verjetnost in logiko s preprostimi vizualnimi primeri.

Vennov diagram je diagram, ki ponazarja logično povezavo med množicami. John Venn jih je populariziral v osemdesetih letih 19. stoletja, zdaj pa se pogosto uporabljajo pri poučevanju in analizah. Uporabljajo se za razlago osnovne teorije množic in za ponazoritev preprostih odnosov med množicami v verjetnosti, logiki, statistiki, jezikoslovju in računalništvu. Vennov diagram uporablja zaprte krivulje, narisane na ravnini, za predstavitev množic; najpogosteje so to krogi ali elipse, pri čemer vsak krogi predstavlja eno množico.

Podobne zamisli so bile predlagane že pred Vennom. Christian Weise leta 1712 (Nucleus Logicoe Wiesianoe) in Leonhard Euler (Pisma nemški princesi) 1768 sta prišla s podobnimi idejami. Zamisel je populariziral Venn v delu Symbolic Logic, Chapter V "Diagrammatic Representation", 1881.

Kaj prikazuje Vennov diagram

Vennov diagram razdeli ravnino na regije, pri čemer vsaka regija ustreza določenemu kombiniranemu položaju elementa glede na množice (npr. v A in v B, v A ampak ne v B itd.). Z Vennovimi diagrami običajno ponazarjamo naslednje operacije množic:

• Unija (A ∪ B): vsi elementi, ki so v A ali v B (ali v obeh).
• Presek (A ∩ B): elementi, ki so hkrati v A in v B.
• Komplement (A^c ali ¬A): elementi, ki niso v A.
• Razlika (A \ B): elementi, ki so v A, vendar ne v B.

Branje in primeri

Najenostavnejši primer je diagram z dvema množicama A in B, kjer sta kroga delno prekrivata. Prekrivajoči del predstavlja A ∩ B, zunanja dela posameznih krogov sta A \ B in B \ A, zunaj obeh krogov pa je univerzalna množica minus (A ∪ B). V praksi se pogosto uporablja primer učencev: kroga predstavljata učence, ki so opravili matematiko oziroma slovenščino; presečišče pokaže tiste, ki sta opravila oba predmeta.

Za tri množice so običajni trije krogi, ki se medsebojno prekrivajo in tvorijo do sedmih različnih neprekrivnih regij (plus regija zunaj vseh treh). Trikratne preseke (A ∩ B ∩ C) so enostavno ponazorjene in pogosto uporabljene za bolj zapletene logične ali statistične primerjave.

Razlika med Eulerjevimi in Vennovimi diagrami

Eulerjevi diagrami in Vennovi diagrami so si podobni, vendar se razlikujeta v pomenu: Eulerjevi diagrami prikazujejo le dejanske ne-prazne odnose med množicami (manj regij, odvisno od relacij), medtem ko Vennovi diagrami eksplicitno prikažejo vse možne kombinacije členov množic, tudi če je katera regija prazna. Zaradi tega so Vennovi diagrami bolj sistematični za učenje in za logične dokaze.

Uporaba v različnih disciplinah

• Verjetnost: Vennovi diagrami pomagajo razumeti verjetnosti kombiniranih dogodkov (npr. P(A ∪ B) = P(A) + P(B) − P(A ∩ B)).
• Logika in teorija množic: Grafično prikazovanje logičnih izjav in dokazovanje identitet (De Morganovi zakoni ipd.).
• Statistika: Vizualizacija prekrivanj med skupinami podatkov.
• Jezikoslovje: Analiza presekov lastnosti besed ali jezikovnih kategorij.
• Računalništvo: Modeliranje Booleanove algebre, iskanje po zbirkah, poizvedbe v podatkovnih bazah in analiza logičnih izrazov.

Napredne različice in omejitve

Sistematično risanje Vennovih diagramov za veliko število množic postane zapleteno. Za štiri in več množic so možne oblike, vendar so pogosto težje berljive; zato se za vizualizacijo več množic včasih uporabljajo druge tehnike (Eulerjevi diagrami, matrike, heatmap-e, uporaba barv in interaktivnih vizualizacij). Obstajajo tudi posebne pomembne konstrukcije, kot so simetrični Vennovi diagrami (za prastevila množic) in topološke različice, ki omogočajo lepo razporeditev mnogih množic.

Kratek vodič: kako narisati preprost Vennov diagram

1. Odločite se, katere množice predstavljate in katero univerzalno množico upoštevate (celoten prostor elementov).
2. Narišite kroge (ali elipse), po en kroge za vsako množico, tako da se ustrezno prekrivajo glede na pričakovane preseke.
3. Označite regije (če želite, z imeni ali števili elementov) in po potrebi obarvajte ali označite tiste regije, ki jih izračunavate (npr. za A ∩ B označite prekrivajoči del).
4. Uporabite diagram za izvedbo računov ali za argumentacijo — npr. preverite, ali je neka identiteta med množicami pravilna glede na ponazoritev.

Zaključek

Vennovi diagrami so preprost in hkrati močan grafični pripomoček za razumevanje odnosov med množicami. So temeljno orodje v izobraževanju in uporabno v številnih znanstvenih in praktičnih disciplinah. Čeprav imajo omejitve pri zelo velikem številu množic, ostajajo ena najbolj intuitivnih metod za vizualizacijo logičnih in množičnih odnosov.

Primer

V naslednjem primeru sta uporabljena dva niza, A in B, ki sta tu predstavljena z barvnimi krogi. Oranžni krog, sklop A, predstavlja vsa živa bitja, ki imajo dve nogi. Modri krog, sklop B, predstavlja živa bitja, ki lahko letijo. Vsako posamezno vrsto bitja si lahko predstavljamo kot točko nekje na diagramu. Živa bitja, ki lahko letijo in imajo hkrati dve nogi, na primer papige, so nato v obeh sklopih, zato ustrezajo točkam na območju, kjer se modri in oranžni krogi prekrivajo. To območje vsebuje vsa takšna in samo takšna živa bitja.

Ljudje in pingvini so dvonožni, zato so v oranžnem krogu, ker pa ne morejo leteti, so v levem delu oranžnega kroga, ki se ne prekriva z modrim krogom. Komarji imajo šest nog in letijo, zato je točka za komarje v delu modrega kroga, ki se ne prekriva z oranžnim. Bitja, ki nimajo dveh nog in ne morejo leteti (na primer kiti in pajki), bi bila predstavljena s točkami zunaj obeh krogov.

Skupno območje množic A in B imenujemo unija A in B, ki jo označimo z A ∪ B. Unija v tem primeru vsebuje vsa živa bitja, ki imajo dve nogi ali lahko letijo (ali oboje). Območje v A in B, kjer se obe množici prekrivata, se imenuje presečišče A in B, označeno z A ∩ B. Na primer, presečišče obeh množic ni prazno, saj obstajajo točke, ki predstavljajo bitja, ki so tako v oranžnem kot modrem krogu.

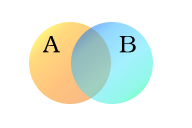
Sklopa A (bitja z dvema nogama) in B (bitja, ki lahko letijo)

Vprašanja in odgovori

V: Kaj je Vennov diagram?

V: Kdo je populariziral Vennove diagrame?

V: Za kaj se uporabljajo?

V: Kdo je pred Johnom Vennom predlagal podobne ideje?

V: Kdaj je John Venn objavil Simbolno logiko?

V: V katerem poglavju Simbolne logike je John Venn populariziral zamisel o Vennovem diagramu?

V: Kako so bile te ideje predstavljene pred iznajdbo sodobne različice V ennovega diagrama?

Išči po črki