Magnetni moment – definicija, dipolni moment in magnetno polje
Magnetni moment — jasna definicija, dipolni moment in magnetno polje: vektorji, lastnosti, primeri (elektron, magnet, planet) ter vpliv na magnetne sile in navor.
Magnetni moment magneta je količina, ki določa silo, s katero lahko magnet deluje na električni tok, in navor, ki ga na magnet deluje magnetno polje. Magnetni moment imajo električni tok, palični magnet, elektron, molekula in planet.
Magnetni moment in magnetno polje lahko obravnavamo kot vektorja, ki imata velikost in smer. Smer magnetnega momenta poteka od južnega proti severnemu polu magneta. Magnetno polje, ki ga ustvarja magnet, je prav tako sorazmerno z njegovim magnetnim momentom. Natančneje, izraz magnetni moment se običajno nanaša na magnetni dipolni moment sistema, ki tvori prvi člen v multipolnem raztezku splošnega magnetnega polja. Dipolna komponenta magnetnega polja predmeta je simetrična glede na smer njegovega magnetnega dipolnega momenta in se zmanjšuje kot obratna kocka razdalje od predmeta.
Definicija in fizični pomen
Magnetni dipolni moment μ opisuje, kako močno in v katero smer magnet (ali tokovna zanka, delce z magnetnim momentom ipd.) povzroča magnetno polje in kako se odziva na zunanje magnetno polje. Vektor μ usmerjen tako, da se magnetni dipol nagiba v smeri zunanjega polja; iz njega izhaja navor in potencialna energija v polju.
Temeljne enačbe in smernice
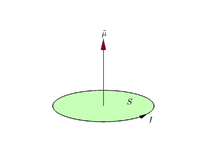
- Magnetni moment za tokovno zanko: μ = I·A·n, kjer je I jakost toka, A površina zanke, n enotski vektor pravokoten na površino (smer določa desna roka glede na smer toka).
- Navor v zunanjm polju: τ = μ × B. Navor poskuša obrniti dipol tako, da se μ poravna z magnetnim poljem B.
- Potencialna energija: U = −μ · B. Najnižja energija je, ko je μ vzporeden z B.
- Magnetno polje dipola v prostem prostoru (SI): B(r) = (μ0/4π) · [ (3(μ·r̂) r̂ − μ) / r^3 ], kjer je r vektor od dipola do točke opazovanja, r̂ enotski vektor, r njegova velikost, in μ0 permeabilnost vakuuma.
Enote in primerjava
- SI enota magnetnega momenta je A·m^2 (amper kvadratni meter). Ta enota je enakovredna J/T (joule na teslo).
- Za atomske in kvantne sisteme se pogosto uporablja Bohrjev magneton μB = eħ/(2m_e) ≈ 9.274×10^−24 J/T kot priročna merska enota za magnetne momente elektronov in atomov.
Magnetni moment delcev in predmetov
- Električna tokovna zanka ali palični magnet: magnetni moment je posledica urejenega gibanja naboja ali urejenih magnetnih domen v trdnem snu.
- Elektron: ima magnetni moment zaradi orbitalnega gibalnega momenta in spina. Zaradi negativnega naboja elektrona je magnetni moment običajno nasproten njegovemu kotnimu gibalnemu momentu.
- Molekule in atomi: lahko imajo neto magnetni moment od nesparjenih elektronov (paramagnetne) ali inducirane nasprotne momente (diamagnetske). Feromagnetne snovi imajo velike stalne magnetne momente zaradi urejenosti domen.
- Planeti: npr. Zemlja ima približno magnetni dipolni moment reda 8×10^22 A·m^2, ki izhaja iz tokov prevodnih tekočin v jedru.
Usmerjenost magnetnega momenta
Smer magnetnega momenta za tokovno zanko določi desna roka: prsti sledijo smeri konvencionalnega toka, palec pa kaže v smer μ. Pri elektronu pa zaradi njegovega negativnega naboja magnetni moment kaže v nasprotni smeri kot njegova komponenta kotnega gibalnega momenta.
Pomen dipola v daljavi
Ker dipolno polje pada kot 1/r^3, na dovolj veliki razdalji višji multipolni momenti (kvadrupol, ok.) hitro postanejo nepomembni in je magnetno polje zunanji videti kot polje enega dipola. To pojasni, zakaj opazovanje zunanjega polja mnogih predmetov omogoča oceno njihovega skupnega dipolnega momenta.
Primeri uporabe in pomenu
- Kompas — magnetni moment igle se poravna z magnetnim poljem Zemlje in kaže smer polov.
- Magnetični materiali — razumevanje magnetnih momentov je ključno pri oblikovanju magnetov, magnetnih trakov in trdnih polovodnikov za shranjevanje podatkov.
- Fizikalne meritve — merjenje magnetnih momentov atomov in molekul daje vpogled v elektronsko strukturo in magnetno obnašanje snovi (npr. ESR, NMR in magnetometrija).
Ključne formule (povzetek)
- μ (tokovna zanka) = I·A·n
- τ = μ × B
- U = −μ · B
- B_dipol(r) = (μ0/4π) · [ (3(μ·r̂) r̂ − μ) / r^3 ]
Magnetni moment je torej temeljna količina za opis magnetnega obnašanja tako v makroskopskih sistemih (magneta, planeti) kot v mikroskopskih (elektroni, atomi, molekule). Razumevanje njegove smeri, velikosti in interakcije z zunanjim poljem omogoča napovedovanje sil, navorov in energetskih razlik, ki nastanejo v magnetnih sistemih.
Dve opredelitvi momenta
V učbenikih se za opredelitev magnetnih momentov uporabljata dva dopolnjujoča se pristopa. V učbenikih pred letom 1930 so jih opredeljevali s pomočjo magnetnih polov. V novejših učbenikih so opredeljeni z Ampèrovimi tokovi.
Opredelitev magnetnega pola
Fiziki predstavljajo vire magnetnih momentov v materialih kot pole. Severni in južni pol sta analogna pozitivnemu in negativnemu naboju v elektrostatiki. Vzemimo za primer palični magnet, ki ima magnetna pola enake velikosti, vendar nasprotne polarnosti. Vsak pol je vir magnetne sile, ki z razdaljo slabi. Ker sta magnetna pola vedno v paru, se njuni sili delno izničita, saj medtem ko en pol vleče, drugi odbija. To izničevanje je največje, kadar sta pola blizu drug drugemu, tj. kadar je palični magnet kratek. Magnetna sila, ki jo ustvarja palični magnet v dani točki v prostoru, je torej odvisna od dveh dejavnikov: od moči p {\displaystyle p}
njegovih polov in od vektorja l {\displaystyle \mathbf {l} }, ki ju 
ločuje. Moment je definiran kot
m = p l . {\displaystyle \mathbf {m} =p\mathbf {l} . } 
Usmerjena je v smeri od južnega do severnega tečaja. Analogije z električnimi dipoli ne smemo jemati predaleč, saj so magnetni dipoli povezani s kotnim momentom (glej Magnetni moment in kotni moment). Kljub temu so magnetni poli zelo uporabni pri magnetostatičnih izračunih, zlasti pri aplikacijah za feromagnetike. Praktiki, ki uporabljajo pristop magnetnih polov, običajno predstavljajo magnetno polje z irotacijskim poljem H {\displaystyle \mathbf {H} } 
po analogiji z električnim poljem E {\displaystyle \mathbf {E} } 
.
Opredelitev tokovne zanke
Predpostavimo, da ravninska zaprta zanka prenaša električni tok I {\displaystyle I}
in ima vektorsko površino S {\displaystyle \mathbf {S} } 
( x {\displaystyle x}
, y {\displaystyle y} 
, in z {\displaystyle z} 
koordinate tega vektorja so površine projekcij zanke na y z {\displaystyle yz} 
, z x {\displaystyle zx} 
in x y {\displaystyle xy}
ravnine). Njen magnetni moment m {\displaystyle \mathbf {m} } 
, vektor, je opredeljen kot:
m = I S . {\displaystyle \mathbf {m} =I\mathbf {S} . } 
Po dogovoru je smer vektorskega območja podana s pravilom desnega prijema (zvijanje prstov desne roke v smeri toka okoli zanke, ko se dlan "dotika" zunanjega roba zanke, ravni palec pa kaže smer vektorskega območja in s tem magnetnega momenta).
Če zanka ni ravninska, je trenutek podan kot
m = I 2∫ r × d r . {\displaystyle \mathbf {m} ={\frac {I}{2}}\int \mathbf {r} \times {\rm {d}}\mathbf {r} . } 
V najbolj splošnem primeru poljubne porazdelitve toka v prostoru lahko magnetni moment takšne porazdelitve ugotovimo iz naslednje enačbe:
m = 12∫ r × J d V , {\displaystyle \mathbf {m} ={\frac {1}{2}}\int \mathbf {r} \times \mathbf {J} \,{\rm {d}}V,} 
kjer r {\displaystyle \mathbf {r} }
je položajni vektor, ki kaže od izvora do lokacije elementa prostornine, in J {\displaystyle \mathbf {J} je položajni vektor, ki kaže od izvora do lokacije elementa prostornine, in J {\displaystyle \mathbf {J} }
je vektor gostote toka na tej lokaciji.
Zgornjo enačbo lahko uporabimo za izračun magnetnega momenta poljubnega sklopa gibajočih se nabojev, kot je vrteča se nabita trdna snov, tako da nadomestimo
J = ρ v , {\displaystyle \mathbf {J} =\rho \mathbf {v} ,} 
kjer je ρ {\displaystyle \rho }
gostota električnega naboja v dani točki, v {\displaystyle \mathbf {v} }
pa trenutna linearna hitrost te točke.
Magnetni moment, ki ga ustvari električni naboj, ki se giblje po krožni poti, je na primer
m = q 12r × v {\displaystyle \mathbf {m} ={\frac {1}{2}}\,q\,\mathbf {r} \times \mathbf {v} } 
,
kjer r {\displaystyle \mathbf {r} } je položaj naboja q {\displaystyle q}
glede na središče kroga, v {\displaystyle \mathbf {v} } pa je trenutna hitrost naboja.
Praktiki, ki uporabljajo model tokovne zanke, običajno predstavljajo magnetno polje s solenoidnim poljem B {\displaystyle \mathbf {B} } 
analogno elektrostatičnemu polju D {\displaystyle \mathbf {D} } 
.
Magnetni moment solenoida
Poenostavitev zgornje tokovne zanke je večvratna tuljava ali solenoid. Njen moment je vektorska vsota momentov posameznih zavojev. Če ima solenoid N {\displaystyle N} 
enakih zavojev (enoslojno navitje),
m = N I S . {\displaystyle \mathbf {m} =NI\mathbf {S} . } 
Tridimenzionalna slika solenoida.
Moment m {\displaystyle \mathbf {m} } ravninske tokovne zanke s površino S {\displaystyle S}
in tokom I {\displaystyle I} .
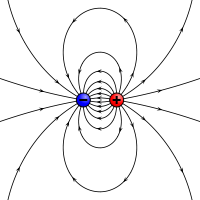
Elektrostatična analogija magnetnega momenta: dva nasprotna naboja, ki sta med seboj ločena na končni razdalji.
Enote
Enota za magnetni moment ni osnovna enota v mednarodnem sistemu enot (SI) in jo je mogoče predstaviti na več načinov. Na primer, v definiciji tokovne zanke se površina meri v kvadratnih metrih, I {\displaystyle I} pa v amperih, zato se magnetni moment meri v kvadratnih metrih v amperih ( A m {\displaystyle2 {\text{A m}}^{2}}
). V enačbi za navor na moment se navor meri v njutonmetrih, magnetno polje pa v teslah, zato se moment meri v N.m na teslo ( N.m T - 1{\displaystyle {\text{N.m T}}^{-1}}
). Ti dve predstavitvi sta enakovredni:
A m = 2N.m T -1 . {\displaystyle \,{\text{A m}}^{2}=\,{\text{N.m T}}^{-1}. } 
V sistemu CGS obstaja več različnih sklopov elektromagnetnih enot, med katerimi so glavne ESU, Gaussian in EMU. Med njimi sta v sistemu CGS dve alternativni (neekvivalentni) enoti za magnetni dipolni moment:
(ESU CGS) 1 statA-cm² = 3,33564095×10-14 (m-A2 ali N.m/T)
in (pogosteje uporabljena)
(EMU CGS in Gaussian-CGS) 1 erg/G = 1 abA-cm² = 10-3 (m-A2 ali N.m/T).
Razmerje teh dveh neekvivalentnih enot CGS (EMU/ESU) je natančno enako hitrosti svetlobe v prostem prostoru, izraženi v cm/s.
Vse formule v tem članku so pravilne v enotah SI, v drugih sistemih enot pa jih bo morda treba spremeniti. V enotah SI ima na primer tokovna zanka s tokom I in površino A magnetni moment I×A (glej spodaj), v Gaussovih enotah pa je magnetni moment I×A/c.
| Lastni magnetni momenti in spini nekaterih elementarnih delcev | ||
| Delci | Magnetni dipolni moment v enotah SI (10 −27J/T) | Spinsko kvantno število (brezrazsežno) |
| -9284.764 | 1/2 | |
| proton | 14.106067 | 1/2 |
| nevtron | -9.66236 | 1/2 |
| mioni | -44.904478 | 1/2 |
| deuteron | 4.3307346 | 1 |
| triton | 15.046094 | 1/2 |
Za povezavo med pojmoma magnetni moment in magnetizacija glej magnetizacija.
Vprašanja in odgovori
V: Kaj je magnetni moment magneta?
O: Magnetni moment magneta je količina, ki določa silo, s katero lahko magnet deluje na električne tokove, in navor, ki ga bo nanj delovalo magnetno polje.
V: Kateri predmeti imajo magnetni moment?
O: Magnetne momente imajo električni tok, palični magnet, elektron, molekula in planet.
V: Kako lahko upoštevamo magnetni moment in magnetno polje?
O: Magnetni moment in magnetno polje lahko obravnavamo kot vektorja, ki imata velikost in smer.
V: V katero smer kaže magnetni moment v magnetu?
O: Smer magnetnega momenta je od južnega do severnega pola magneta.
V: Kakšno je razmerje med magnetnim momentom in magnetnim poljem magneta?
O: Magnetno polje, ki ga ustvarja magnet, je sorazmerno z njegovim magnetnim momentom.
V: Na kaj se običajno nanaša izraz magnetni moment?
O: Natančneje, izraz magnetni moment se običajno nanaša na magnetni dipolni moment sistema, ki tvori prvi člen v multipolnem razširjanju splošnega magnetnega polja.
V: Kako se obnaša dipolna komponenta magnetnega polja predmeta, ko se oddaljenost od predmeta povečuje?
O: Dipolna komponenta magnetnega polja predmeta je simetrična glede na smer magnetnega dipolnega momenta in se zmanjšuje kot obratna kocka razdalje od predmeta.
Iskati