Harmonična vrsta

Zgodovina

Dejstvo, da se harmonske vrste razhajajo, je v 14. stoletju prvič dokazal Nicole Oresme, vendar je bilo pozabljeno. Dokaze so v 17. stoletju podali Pietro Mengoli, Johann Bernoulli in Jacob Bernoulli.

Harmonična zaporedja so uporabljali arhitekti. V obdobju baroka so jih arhitekti uporabljali v razmerjih tlorisov in višinskih gabaritov ter v razmerjih med arhitekturnimi detajli cerkva in palač.

Divergenca

Obstaja več znanih dokazov za divergentnost harmonske vrste. Nekaj jih je navedenih v nadaljevanju.

Primerjalni test

Eden od načinov dokazovanja divergence je primerjava harmonske vrste z drugo divergentno vrsto, kjer je vsak imenovalec nadomeščen z naslednjo največjo močjo dveh:

1 + 1 2 + 1 3 + 1 4 + 1 5 + 1 6 + 1 7 + 1 8 + 1 9 + ⋯ ≥ 1 + 1 2 + 1 4 + 1 4 + 1 8 + 1 8 + 1 8 + 1 8 + 1 8 + 1 16 + ⋯ {\displaystyle {\begin{aligned}&{}1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}}+{\frac {1}{6}}+{\frac {1}{7}}+{\frac {1}{8}}+{\frac {1}{9}}+\cdots \\[12pt]\geq {}&1+{\frac {1}{2}}+{\frac {1}{\color {red}{\mathbf {4} }}}+{\frac {1}{4}}+{\frac {1}{\color {red}{\mathbf {8}} }}}+{{\frac {1}{\color {red}{\mathbf {8}} }}}+{{\frac {1}{\color {red}{\mathbf {8}} }}}+{\frac {1}{8}}+{\frac {1}{\color {red}{\mathbf {16}} }}}+\cdots \end{aligned}}}

Vsak člen harmonske vrste je večji ali enak ustreznemu členu druge vrste, zato mora biti vsota harmonske vrste večja ali enaka vsoti druge vrste. Vendar je vsota druge vrste neskončna:

1 + ( 1 2 ) + ( 1 4 + 1 4 ) + ( 1 8 + 1 8 + 1 8 + 1 8 ) + ( 1 16 + ⋯ + 1 16 ) + ⋯ = 1 + 1 2 + 1 2 + 1 2 + 1 2 + ⋯ = ∞ {\displaystyle {\begin{aligned}&{}1+\left({\frac {1}{2}}\right)+\left({\frac {1}{4}}\!+\!{\frac {1}{4}}}\right)+\left({\frac {1}{8}}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\!+\!{\frac {1}{8}}\desno)+\levo({\frac {1}{16}}\!+\!\cdots \!+\!{\frac {1}{16}}\desno)+\cdots \\[12pt]={}&1+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+{\frac {1}{2}}+\cdots =\infty \end{aligned}}}

Iz tega sledi (s primerjalnim testom), da mora biti tudi vsota harmonskih vrst neskončna. Natančneje, zgornja primerjava dokazuje, da

∑ n = 1 2 k 1 n ≥ 1 + k 2 {\displaystyle \sum _{n=1}^{2^{k}}{\frac {1}{n}}\geq 1+{\frac {k}{2}}}

za vsako pozitivno celo število k.

Ta dokaz, ki ga je okoli leta 1350 predlagal Nicole Oresme, velja za vrhunec srednjeveške matematike. Še danes je standardni dokaz, ki se poučuje pri pouku matematike.

Integralni preskus

Dokazati je mogoče, da se harmonska vrsta razhaja, tako da njeno vsoto primerjamo z nepravim integralom. Upoštevaj razporeditev pravokotnikov, ki je prikazana na sliki desno. Vsak pravokotnik je širok 1 enoto in visok 1/n enot, zato je skupna površina neskončnega števila pravokotnikov enaka vsoti harmonske vrste:

površina pravokotnikov = 1 + 1 2 + 1 3 + 1 4 + 1 5 + ⋯ {\displaystyle {\begin{array}{c}{\text{površina}}\\{\text{pravokotniki}}\\end{array}}=1+{\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{4}}+{\frac {1}{5}}}+\cdots }

Celotno površino pod krivuljo y = 1/x od 1 do neskončnosti določa divergentni nepravi integral:

površina pod krivuljo = ∫ 1 ∞ 1 x d x = ∞ . {\displaystyle {\begin{array}{c}{\text{površina pod}}}\\{\text{krivuljo}}\end{array}}}=\int _{1}^{\infty }{\frac {1}{x}}},dx=\infty . }

Ker je ta površina v celoti zajeta v pravokotnikih, mora biti tudi skupna površina pravokotnikov neskončna. To dokazuje, da

∑ n = 1 k 1 n > ∫ 1 k + 1 1 1 x d x = ln ( k + 1 ) . {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}>\int _{1}^{k+1}{\frac {1}{x}}\,dx=\ln(k+1). }

Posplošitev tega argumenta je znana kot integralni test.

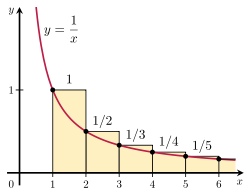
Ilustracija integralnega testa.

Stopnja razhajanja

Harmonska vrsta se razhaja zelo počasi. Vsota prvih 1043 členov je na primer manjša od 100. To je zato, ker imajo delne vsote vrste logaritemsko rast. Zlasti,

∑ n = 1 k 1 n = ln k + γ + ε k ≤ ( ln k ) + 1 {\displaystyle \sum _{n=1}^{k}{\frac {1}{n}}=\ln k+\gama +\varepsilon _{k}\leq (\ln k)+1}

kjer je γ Euler-Mascheronijeva konstanta in εk ~ 1/2k, ki se pri neskončnosti k približuje 0. Leonhard Euler je dokazal to in tudi to, da se vsota, ki vključuje samo recipročne vrednosti praštevil, prav tako odmika, tj:

∑ p prime 1 p = 1 2 + 1 3 + 1 5 + 1 7 + 1 11 + 1 13 + 1 17 + ⋯ = ∞ . {\displaystyle \sum _{p{\text{ prime }}}{\frac {1}{p}}={\frac {1}{2}}+{\frac {1}{3}}+{\frac {1}{5}}}+{\frac {1}{7}}+{\frac {1}{11}}+{\frac {1}{13}}}+{\frac {1}{17}}+\cdots =\infty . }

Delne vsote

Prvih trideset harmonskih števil
n	Delna vsota harmonske vrste, Hn
	izražen kot delež		decimalno	relativna velikost
1	1		~1	1
2	3	/2	~1.5	1.5
3	11	/6	~1.83333	1.83333
4	25	/12	~2.08333	2.08333
5	137	/60	~2.28333	2.28333
6	49	/20	~2.45	2.45
7	363	/140	~2.59286	2.59286
8	761	/280	~2.71786	2.71786
9	7129	/2520	~2.82897	2.82897
10	7381	/2520	~2.92897	2.92897
11	83711	/27720	~3.01988	3.01988
12	86021	/27720	~3.10321	3.10321
13	1145993	/360360	~3.18013	3.18013
14	1171733	/360360	~3.25156	3.25156
15	1195757	/360360	~3.31823	3.31823
16	2436559	/720720	~3.38073	3.38073
17	42142223	/12252240	~3.43955	3.43955
18	14274301	/4084080	~3.49511	3.49511
19	275295799	/77597520	~3.54774	3.54774
20	55835135	/15519504	~3.59774	3.59774
21	18858053	/5173168	~3.64536	3.64536
22	19093197	/5173168	~3.69081	3.69081
23	444316699	/118982864	~3.73429	3.73429
24	1347822955	/356948592	~3.77596	3.77596
25	34052522467	/8923714800	~3.81596	3.81596
26	34395742267	/8923714800	~3.85442	3.85442
27	312536252003	/80313433200	~3.89146	3.89146
28	315404588903	/80313433200	~3.92717	3.92717
29	9227046511387	/2329089562800	~3.96165	3.96165
30	9304682830147	/2329089562800	~3.99499	3.99499

Končne delne vsote razhajajočih se harmonskih vrst,

H n = ∑ k = 1 n 1 k , {\displaystyle H_{n}=\sum _{k=1}^{n}{\frac {1}{k}}},}

imenujemo harmonična števila.

Razlika med Hn in ln n konvergira k Euler-Mascheronijevi konstanti. Razlika med katerima koli dvema harmoničnima številoma ni nikoli celo število. Nobeno harmonsko število ni celo število, razen _H1 = 1.

Sorodne serije

Izmenična harmonska serija

Serija

∑ n = 1 ∞ ( - 1 ) n + 1 n = 1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ {\displaystyle \sum _{n=1}^{\infty }{\frac {(-1)^{n+1}}{n}}=1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots }

je znana kot izmenična harmonska vrsta. Ta vrsta konvergira s preskusom izmenične vrste. Zlasti je vsota enaka naravnemu logaritmu števila 2:

1 - 1 2 + 1 3 - 1 4 + 1 5 - ⋯ = ln 2. {\displaystyle 1-{\frac {1}{2}}+{\frac {1}{3}}-{\frac {1}{4}}+{\frac {1}{5}}-\cdots =\ln 2.}

Čeprav je izmenična harmonska vrsta pogojno konvergentna, ni absolutno konvergentna: če člene v vrsti sistematično preuredimo, se vsota na splošno spremeni in, odvisno od preureditve, lahko postane celo neskončna.

Formula izmenične harmonske vrste je poseben primer Mercatorjeve vrste, Taylorjeve vrste za naravni logaritem.

Sorodno vrsto lahko izpeljemo iz Taylorjeve vrste za arktangent:

∑ n = 0 ∞ ( - 1 ) n 2 n + 1 = 1 - 1 3 + 1 5 - 1 7 + ⋯ = π 4 . {\displaystyle \sum _{n=0}^{\infty }{\frac {(-1)^{n}}{2n+1}}}=1-{\frac {1}{3}}+{\frac {1}{5}}-{\frac {1}{7}}+\cdots ={\frac {\pi }{4}}. }

To je znano kot Leibnizova vrsta.

Splošne harmonske vrste

Splošna harmonska vrsta ima obliko

∑ n = 0 ∞ 1 a n + b , {\displaystyle \sum _{n=0}^{\infty }{\frac {1}{an+b}},}

kjer sta a ≠ 0 in b realni števili, b/a pa ni nič ali negativno celo število.

S testom mejne primerjave s harmonsko vrsto se razhajajo tudi vse splošne harmonske vrste.

serija p

Poenostavitev harmonske vrste je p-vrsta (ali hiperharmonska vrsta), ki je definirana kot

∑ n = 1 ∞ 1 n p {\displaystyle \sum _{n=1}^{\infty }{\frac {1}{n^{p}}}}

za katero koli realno število p. Če je p = 1, je p-vrsta harmonična vrsta, ki se odmika. Integralni test ali Cauchyjev kondenzacijski test pokažeta, da vrsta p konvergira za vse p > 1 (v tem primeru jo imenujemo nadharmonična vrsta) in divergira za vse p ≤ 1. Če je p > 1, potem je vsota p-vrste ζ(p), to je Riemannova zeta funkcija, ocenjena pri p.

Problem iskanja vsote za p = 2 se imenuje Baslov problem; Leonhard Euler je pokazal, da je vsota π2/6. Vrednost vsote za p = 3 se imenuje Apéryjeva konstanta, saj je Roger Apéry dokazal, da je to iracionalno število.

serije ln

Z vrsto p je povezana vrsta ln, ki je opredeljena kot

∑ n = 2 ∞ 1 n ( ln n ) p {\displaystyle \sum _{n=2}^{\infty }{\frac {1}{n(\ln n)^{p}}}}

za vsako pozitivno realno število p. To je mogoče dokazati s testom integralov, ki se razhaja za p ≤ 1, vendar konvergira za vse p > 1.

serije φ

Za vsako konveksno, realno vrednostno funkcijo φ, ki je

lim sup u → 0 + φ ( u 2 ) φ ( u ) < 1 2 , {\displaystyle \limsup _{u\to 0^{+}}{\frac {\varphi \left({\frac {u}{2}}} desno)}{\varphi (u)}}<{\frac {1}{2}},}

serija

∑ n = 1 ∞ φ ( 1 n ) {\displaystyle \sum _{n=1}^{\infty }\varphi \left({\frac {1}{n}}}\right)}

je konvergentna. ^[]

Naključne harmonske vrste

Naključna harmonska vrsta

∑ n = 1 ∞ s n n , {\displaystyle \sum _{n=1}^{\infty }{\frac {s_{n}}{n}},}

kjer so _sn neodvisne, identično porazdeljene naključne spremenljivke, ki imajo vrednosti +1 in -1 z enako verjetnostjo 1/2, je v teoriji verjetnosti znan primer vrste naključnih spremenljivk, ki konvergira z verjetnostjo 1. Dejstvo te konvergence je enostavna posledica Kolmogorovega teorema o treh vrstah ali tesno povezane Kolmogorove maksimalne neenakosti. Byron Schmuland z Univerze v Alberti je nadalje preučil lastnosti naključne harmonične vrste in pokazal, da je konvergentna vrsta naključna spremenljivka z nekaterimi zanimivimi lastnostmi. Zlasti funkcija gostote verjetnosti te naključne spremenljivke, ocenjena pri +2 ali pri -2, ima vrednost 0,12499999999999999999999999999999764 ..., ki se od 1/8 razlikuje za manj kot 10-42. Schmulandov članek pojasnjuje, zakaj je ta verjetnost tako blizu 1/8, vendar ne točno. Natančna vrednost te verjetnosti je podana z integralom neskončnega kosinusnega produkta _C2, deljenega s π.

Izčrpana harmonska serija

Izčrpana harmonska vrsta, pri kateri so odstranjeni vsi členi, v katerih se kjer koli v imenovalcu pojavi števka 9, konvergira, njena vrednost pa je manjša od 80. Dejansko, ko odstranimo vse člene, ki vsebujejo določen niz številk (v katerikoli osnovi), vrsta konvergira.

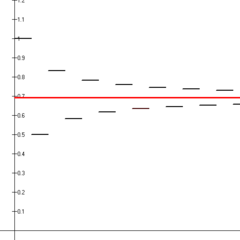
Prvih štirinajst delnih vsot izmenične harmonske vrste (črni deli črte), ki konvergirajo k naravnemu logaritmu 2 (rdeča črta).

Aplikacije

Harmonska vrsta je lahko kontraintuitivna. To je zato, ker gre za divergentno vrsto, čeprav se členi vrste zmanjšujejo in približujejo ničli. Divergentnost harmonske vrste je vir nekaterih paradoksov.

• "Črv na gumijastem traku". Predpostavimo, da se črv plazi po neskončno elastičnem enometrskem gumijastem traku hkrati z enakomernim raztegovanjem gumijastega traku. Če črv potuje 1 centimeter na minuto, trak pa se razteza 1 meter na minuto, ali bo črv kdaj dosegel konec gumijastega traku? Odgovor je nasprotno od intuicije "da", saj je po n minutah razmerje med razdaljo, ki jo prepotuje črv, in celotno dolžino gumijastega traku

1 100 ∑ k = 1 n 1 k . {\displaystyle {\frac {1}{100}}\sum _{k=1}^{n}{\frac {1}{k}}. }

Ker se vrsta z večanjem n poljubno povečuje, mora to razmerje na koncu preseči 1, kar pomeni, da črv doseže konec gumijastega traku. Vendar mora biti vrednost n, pri kateri se to zgodi, izjemno velika: približno e100, kar je število, ki presega 1043 minut (1037 let). Čeprav se harmonska vrsta res oddaljuje, se to dogaja zelo počasi.

• Problem Jeep se sprašuje, koliko skupnega goriva potrebuje avtomobil z omejeno zmogljivostjo za prevoz goriva, da prevozi puščavo in na poti pusti kapljice z gorivom. Razdalja, ki jo avto lahko prevozi z določeno količino goriva, je povezana z delnimi vsotami harmonskih vrst, ki rastejo logaritemsko. Tako potrebno gorivo eksponentno narašča z želeno razdaljo.

• Problem zlaganja kock: če imamo zbirko enakih kock domina, jih je mogoče zložiti na rob mize tako, da visijo čez rob mize, ne da bi padle. Protiintuitivni rezultat je, da jih je mogoče zložiti tako, da je previs poljubno velik. To velja, če je domino kock dovolj.

• Plavalec, ki je hitrejši vsakič, ko se dotakne stene bazena. Plavalec začne plavati čez 10-metrski bazen s hitrostjo 2 m/s, z vsakim prečkanjem pa se mu hitrost poveča še za 2 m/s. Teoretično je hitrost plavalca neomejena, vendar je število prečkanj bazena, potrebnih za dosego te hitrosti, zelo veliko; na primer, da bi plavalec dosegel hitrost svetlobe (ob neupoštevanju posebne teorije relativnosti), mora bazen prečkati 150 milijonkrat. V nasprotju s tem velikim številom je čas, potreben za doseganje določene hitrosti, odvisen od vsote vrst pri poljubnem številu prečkanj bazena:

10 2 ∑ k = 1 n 1 k . {\displaystyle {\frac {10}{2}}\sum _{k=1}^{n}{\frac {1}{k}}. }

Izračun vsote pokaže, da je čas, potreben za doseganje svetlobne hitrosti, le 97 sekund.

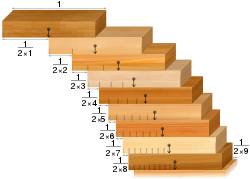
Problem zlaganja blokov: bloki, poravnani v skladu s harmonsko vrsto, premostijo razcepe poljubne širine.

Sorodne strani

• Harmonično napredovanje
• Seznam vsot recipročnih števil