Površinski integral: definicija, lastnosti in uporaba v matematiki in fiziki
Površinski integral: jasna definicija, ključne lastnosti in konkretne uporabe v matematiki ter fiziki — vodič za razumevanje in praktične primere.
V matematiki je površinski integral določen integral, ki se uporablja na površini (ta površina je lahko zvezna gladka ploskev ali pa lokalno obnaša kot krivulja v prostoru). Podobno kot pri linijskem integralu, kjer integriramo po eni dimenziji, si lahko površinski integral predstavljamo kot dvojni integral po dveh dimenzijah. Ob dani površini lahko integriramo skalarna polja (to so funkcije, ki vračajo števila kot vrednosti) in vektorska polja (to so funkcije, ki vračajo vektorje kot vrednosti). Površinski integrali imajo široko uporabo v fiziki, zlasti v klasični teoriji elektromagnetizma, kjer merimo na primer tok ali pretok polja skozi površino.
Osnovni pojmi in definicije
Površina S v prostoru običajno predstavljamo s parametrizacijo r(u,v) = (x(u,v), y(u,v), z(u,v)), kjer (u,v) poteka po nekem obsegu D v ravnini. Element površine (ploskovna mera) pri tej parametrizaciji je
dS = |r_u × r_v| dudv,
kjer r_u in r_v označujeta parcialne odvodnice funkcije r glede na u oziroma v, križni produkt pa daje vektor, katerega velikost ustreza ploščini elementa površine.
Skalarni površinski integral funkcije f nad površino S je definiran kot dvojni integral po parametričnem območju D:
∬_S f dS = ∬_D f(r(u,v)) |r_u × r_v| dudv.
Vektorski površinski integral (ali pretok vektorskega polja F skozi S) uporablja vektorski element površine n dS ali neposredno križni produkt:
Φ = ∬_S F · n dS = ∬_D F(r(u,v)) · (r_u × r_v) dudv,
kjer je n enota normale (izberi usmeritev: n ali −n) in r_u × r_v je usmerjen vektor elementa površine; pri zamenjavi parametrov se smer lahko spremeni za minus.
Izračun v primeru grafa funkcije
Če je S graf funkcije z = f(x,y) nad območjem D v ravnini xy, potem je parametrična oblika r(x,y) = (x, y, f(x,y)) in element površine:
dS = √(1 + f_x^2 + f_y^2) dA,
torej
∬_S f(x,y,z) dS = ∬_D f(x,y,f(x,y)) √(1 + f_x^2 + f_y^2) dA.
Lastnosti površinskih integralov
- Linearnost: ∬_S (a f + b g) dS = a ∬_S f dS + b ∬_S g dS za skalarna polja; podobno velja za vektorska polja pri vsoti komponent.
- Addivnost: Če je S = S1 ∪ S2 z navidezno prekrivanjem le na meji, je integral preko S vsota integralov preko S1 in S2.
- Odvisnost od orientacije: Skalarni površinski integral (merjenje vsote vrednosti po površini) je neodvisen od izbire normale. Vektorski površinski integral (pretok) pa je odvisen od orientacije — preobrnitev normale spremeni predznak integrala.
- Obnašanje pri parametričnih zamenjavah: Pri parametričnih preslikavah je element površine množen z absolutno vrednostjo Jacobijevega determinantnega izraza |r_u × r_v|, kar zagotavlja pravilno merjenje ploskovnih elementov.
Kaj računamo in kako v praksi
Koraki za izračun površinskega integrala pogosto vključujejo:
- 1) Izberemo primerno parametrično predstavitev S: r(u,v).
- 2) Izračunamo parcialne odvode r_u, r_v in njihov križni produkt r_u × r_v.
- 3) Pri skalarju vstavimo f(r(u,v)) in pomnožimo z |r_u × r_v|; pri vektorju vzamemo skalarni produkt F(r(u,v)) · (r_u × r_v).
- 4) Integriramo po parametričnem območju D v (u,v)-ravnini.
Povezave s fundamentalnimi izreki
- Gaussov (divergenčni) izrek: Pretok polja F skozi zaprto površino S (število krožnih linij navzven) je enak integral po volumnu divergenci: ∬_S F·n dS = ∭_V div F dV. Ta izrek je temelj pri uporabi veleznanosti, zlasti v elektrodinamiki (Gaussov zakon).
- Stokesov izrek: Povezuje linijski integral okoli robne krivulje ∂S s površinskim integralom vrtilne količine (curl): ∮_∂S F·dr = ∬_S (curl F)·n dS. S tem se povezujeta površinski in linijski integrali.
Primeri
1) Površinski integral skalarja na sferi: Za enotsko sfero S in f ≡ 1 je površina ∬_S 1 dS = 4π (za polmer 1). Če je f(θ,φ) podana v sferičnih koordinatah, se uporablja parametrična oblika r(θ,φ) in element dS = R^2 sin θ dθ dφ.
2) Pretok električnega polja skozi zaprto površino: V elektrostatičnem primeru Gaussov zakon pove, da je pretok električnega polja E skozi zaprto površino enak Q/ε0, kjer je Q skupni naboj znotraj površine.
Uporaba v fiziki in inženirstvu
Površinski integrali so ključni pri izračunu pretoka snovi, toplote, naboja ali magnetnega polja skozi površine. Uporabljajo se tudi pri določanju površinskih mas, momentov in pri reševanju parcialnih diferencialnih enačb z mejami, kjer so pogoji postavljeni na površinah. V inženirstvu se pojavljajo pri simulacijah pretočnih polj, elektrostatike, magnetostatike in pri analizi struktur.
Nasveti in pogosto narejene napake
- Vedno preverite, ali površina potrebuje usmeritev (normalo) — to je pomembno pri vektorskih integralih.
- Pri grafih z = f(x,y) uporabite poenostavljeno formulo dS = √(1 + f_x^2 + f_y^2) dA, kadar je to mogoče.
- Pri zaprtih površinah pogosto izkoristite Gaussov izrek, da se izognete neposrednemu računskemu izračunu kompleksnih površin.
Če želite, lahko v nadaljevanju prikažem korak‑po‑korak izračun konkretnega primera (npr. pretok polja F(x,y,z) skozi del sferne površine ali površinski integral skalarja na grafu z = f(x,y)).

Definicija površinskega integrala temelji na razdelitvi površine na majhne površinske elemente.

Prikaz posameznega elementa površine. Ti elementi so s postopkom omejevanja neskončno majhni, da se približajo površini.
Površinski integrali skalarnih polj
Razmislite o površini S, na kateri je definirano skalarno polje f. Če si predstavljamo, da je S izdelana iz neke snovi in je za vsak x v S število f(x) gostota snovi na x, potem je površinski integral f nad S masa na enoto debeline S. (To velja le, če je površina neskončno tanka lupina.) Eden od pristopov k izračunu površinskega integrala je, da površino razdelimo na veliko zelo majhnih delov, predpostavimo, da je na vsakem delu gostota približno konstantna, ugotovimo maso na enoto debeline vsakega dela tako, da pomnožimo gostoto dela z njegovo površino, nato pa dobljena števila seštejemo in ugotovimo skupno maso na enoto debeline S.
Da bi našli eksplicitno formulo za površinski integral, matematiki parametrizirajo S tako, da na S upoštevajo sistem krivuljnih koordinat, kot sta zemljepisna širina in dolžina na krogli. Naj bo takšna parametrizacija x(s, t), pri čemer se (s, t) spreminja v nekem območju T v ravnini. Potem je površinski integral podan z
∫ S f d S = ∬ T f ( x ( s , t ) ) | ∂ x ∂ s × ∂ x ∂ t | d s d t {\displaystyle \int _{S}f\,dS=\iint _{T}f(\mathbf {x} (s,t))\left|{\partial \mathbf {x} \over \partial s}\krat {\partial \mathbf {x} \over \partial t}\desno|ds\,dt}
kjer je izraz med črticami na desni strani velikost navzkrižnega produkta parcialnih derivatov x(s, t).
Če želimo na primer ugotoviti površino neke splošne funkcionalne oblike, na primer z = f ( x , y ) {\displaystyle z=f\,(x,y)}
A = ∫ S d S = ∬ T ‖ ∂ r ∂ x × ∂ r ∂ y ‖ d x d y {\displaystyle A=\int _{S}\,dS=\iint _{T}\left\|{\partial \mathbf {r} \over \partial x}\krat {\partial \mathbf {r} \over \partial y}\\right\|dx\,dy}
kjer je r = ( x , y , z ) = ( x , y , f ( x , y ) ) {\displaystyle \mathbf {r} =(x,y,z)=(x,y,f(x,y))}


A = ∬ T ‖ ( 1 , 0 , ∂ f ∂ x ) × ( 0 , 1 , ∂ f ∂ y ) ‖ d x d y = ∬ T ‖ ( - ∂ f ∂ x , - ∂ f ∂ y , 1 ) ‖ d x d y = ∬ T ( ∂ f ∂ x ) 2 + ( ∂ f ∂ y ) 2 + 1 d x d y {\displaystyle {\begin{aligned}A&{}=\iint _{T}\left\|\left(1,0,{\partial f \over \partial x}\right)\times \left(0,1,{\partial f \over \partial y}\right)\right\|dx\,dy\\&{}=\iint _{T}\left\|\left(-{\partial f \over \partial x},-{\partial f \over \partial y},1\right)\right\|dx\,dy\\&{}=\iint _{T}{\sqrt {\left({\partial f \over \partial x}\right)^{2}+\left({\partial f \over \partial y}\right)^{2}+1}}}\,\,dx\,dy\end{aligned}}}
ki je formula za površino splošne funkcionalne oblike. Vektor v drugi vrstici zgoraj lahko prepoznamo kot normalni vektor na površino.
Upoštevajte, da zgornje formule zaradi navzkrižnega produkta veljajo le za površine, ki so vgrajene v tridimenzionalni prostor.
Površinski integrali vektorskih polj
Vzemimo vektorsko polje v na S, tj. za vsak x v S je v(x) vektor.
Površinski integral je mogoče definirati komponentno v skladu z definicijo površinskega integrala skalarnega polja; rezultat je vektor. To na primer velja za električno polje v neki fiksni točki zaradi električno nabite površine ali za gravitacijo v neki fiksni točki zaradi plasti materiala. Z njim lahko izračunamo tudi magnetni tok skozi površino.
Matematiki lahko integrirajo tudi normalno komponento vektorskega polja; rezultat je skalar. Primer je tekočina, ki teče skozi S, tako da v(x) določa hitrost tekočine pri x. Tok je opredeljen kot količina tekočine, ki steče skozi S v časovni enoti.
Iz tega prikaza sledi, da je tok enak nič, če je vektorsko polje v vsaki točki tangentno na S, saj tekočina teče le vzporedno s S, ne pa niti navznoter niti navzven. To pomeni tudi, da če v ne teče samo vzdolž S, tj. če ima v tangencialno in normalno komponento, potem k toku prispeva samo normalna komponenta. Na podlagi tega razmišljanja moramo za določitev pretoka v v vsaki točki izvesti točkovni produkt v z enotsko površinsko normalo na S, s čimer dobimo skalarno polje, in dobljeno polje integrirati, kot je opisano zgoraj. Tako dobimo formulo
∫ S v ⋅ d S = ∫ S ( v ⋅ n ) d S = ∬ T v ( x ( s , t ) ) ⋅ ( ∂ x ∂ s × ∂ x ∂ t ) d s d t . {\displaystyle \int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }=\int _{S}({\mathbf {v} }\cdot {\mathbf {n} })\,dS=\iint _{T}{\mathbf {v} }(\mathbf {x} (s,t))\cdot \left({\partial \mathbf {x} \over \partial s}\krat {\partial \mathbf {x} \over \partial t}\desno)ds\,dt. }
Presečni produkt na desni strani tega izraza je površinska normala, ki jo določa parametrizacija.
Ta formula določa integral na levi strani (upoštevajte piko in vektorski zapis za element površine).
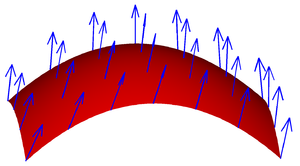
Vektorsko polje na površini.
Teme, ki vključujejo površinske integrale
Z uporabo diferencialne geometrije in vektorskega računa lahko izpeljemo različne uporabne rezultate za površinske integrale, kot sta teorem o divergenci in njegova posplošitev, Stokesov teorem.
Napredna vprašanja
Spreminjanje parametrizacije
V zgornji razpravi je bil površinski integral opredeljen z uporabo parametrizacije površine S. Dana površina ima lahko več parametrizacij. Na primer, če na krogli premaknemo lokaciji severnega in južnega tečaja, se za vse točke na krogli spremenita zemljepisna širina in dolžina. Naravno vprašanje je torej, ali je definicija integralnega števila površine odvisna od izbrane parametrizacije. Za integrale skalarnih polj je odgovor na to vprašanje preprost: vrednost površinskega integrala bo enaka ne glede na to, katero parametrizacijo uporabimo.
Integrali vektorskih polj so bolj zapleteni, saj je vključena površinska normala. Matematiki so dokazali, da če imamo dve parametrizaciji iste površine, katerih površinske normale kažejo v isto smer, obe parametrizaciji dajeta enako vrednost površinskega integrala. Če pa normale teh parametrizacij kažejo v nasprotnih smereh, je vrednost površinskega integrala, dobljena z eno parametrizacijo, negativna od vrednosti, dobljene z drugo parametrizacijo. Iz tega sledi, da se nam pri dani površini ni treba držati nobene edinstvene parametrizacije, vendar pa se moramo pri integriranju vektorskih polj vnaprej odločiti, v katero smer bo kazala normala, in nato izbrati katero koli parametrizacijo, ki je skladna s to smerjo.
Parametrizacije delujejo na delih površine
Druga težava je, da včasih površine nimajo parametriziranja, ki bi pokrivalo celotno površino; to velja na primer za površino valja (končne višine). Očitna rešitev je, da površino razdelimo na več delov, izračunamo površinski integral za vsak del in nato vse seštejemo. Tako stvari dejansko delujejo, vendar je treba pri integriranju vektorskih polj ponovno paziti, kako izbrati normalni vektor za vsak del površine, da so rezultati, ko dele ponovno sestavimo skupaj, skladni. Za valj to pomeni, da če se odločimo, da bo normala za stransko območje kazala ven iz telesa, potem mora normala kazati ven iz telesa tudi za zgornji in spodnji krožni del.
Nedosledne normale površine
Nazadnje, obstajajo površine, ki nimajo površinske normale v vsaki točki, kar daje skladne rezultate (na primer Möbiusov trak). Če takšno površino razdelimo na dele, za vsak del izberemo parametrizacijo in ustrezno površinsko normalo ter dele ponovno sestavimo, se normalni vektorji, ki izhajajo iz različnih delov, ne morejo uskladiti. To pomeni, da bosta na nekem stičišču med dvema deloma normalna vektorja kazala v nasprotnih smereh. Takšno površino imenujemo neorientirana. Vektorskih polj ni mogoče integrirati na neorientiranih površinah.
Sorodne strani
- Teorem o divergenci
- Stokesov teorem
- Linijski integral
- Integralni volumen
- kartezični koordinatni sistem
- Elementi prostornine in površine v sferičnem koordinatnem sistemu
- Elementi prostornine in površine v cilindričnem koordinatnem sistemu
- Holstein-Herringova metoda
Iskati



