Produkt pike

Opredelitev

Točkovni produkt dveh vektorjev a = [a₁ , a₂ , ..., a_n ] in b = [b₁ , b₂ , ..., b_n ] je definiran kot:

a ⋅ b = ∑ i = 1 n a i b i = a 1 b 1 + a 2 b 2 + ⋯ + a n b n {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum _{i=1}^{n}a_{i}b_{i}=a_{1}b_{1}+a_{2}b_{2}+\cdots +a_{n}b_{n}}

kjer Σ pomeni seštevanje (vsota vseh členov), n pa je dimenzija vektorskega prostora.

V razsežnosti 2 je točkovni produkt vektorjev [a,b] in [c,d] ac + bd. Enako je v razsežnosti 3 točkovni produkt vektorjev [a,b,c] in [d,e,f] ad + be + cf. Na primer, točkovni produkt dveh trirazsežnih vektorjev [1, 3, -5] in [4, -2, -1] je

[ 1 , 3 , - 5 ] ⋅ [ 4 , - 2 , - 1 ] = ( 1 × 4 ) + ( 3 × ( - 2 ) ) + ( ( ( - 5 ) × ( - 1 ) ) = ( 4 ) - ( 6 ) + ( 5 ) = 3. {\displaystyle [1,3,-5]\cdot [4,-2,-1]=(1\times 4)+(3\times (-2))+((-5)\times (-1))=(4)-(6)+(5)=3.}

Geometrijska interpretacija

V evklidski geometriji so točkovni produkt, dolžina in kot povezani. Za vektor a je točkovni produkt a - a kvadrat dolžine a ali

a ⋅ a = ‖ a ‖ 2 {\displaystyle {\mathbf {a} \cdot \mathbf {a} }=\levo\|\mathbf {a} \right\|^{2}}

kjer ||a| označuje dolžino (velikost) a. Na splošno, če je b drug vektor

a ⋅ b = ‖ a ‖ ‖ b ‖ cos θ {\displaystyle \mathbf {a} \cdot \mathbf {b} =\levo\|\mathbf {a} \desno\|\,\levo\|\mathbf {b} \right\|\\cos \theta \,}

kjer ||a|| in ||b| označujeta dolžini točk a in b, θ pa je kot med njima.

To formulo lahko preuredimo, da določimo velikost kota med dvema neničelnima vektorjema:

θ = arccos ( a ⋅ b ‖ a ‖ ‖ b ‖ ) {\displaystyle \theta =\arccos \left({\frac {{\mathbf {a}}\cdot {\mathbf {b}}}{\left\|{\mathbf {a}}\right\|\left\|{\mathbf {b}}\right\|}}\right)}

Vektorje lahko najprej pretvorimo v enotske vektorje tako, da jih delimo z njihovo magnitudo:

a ^ = a ‖ a ‖ {\displaystyle {\boldsymbol {\hat {a}}}={\frac {\mathbf {a}}{\left\|{\mathbf {a}}\right\|}}}

potem je kot θ podan z

θ = arccos ( a ^ ⋅ b ^ ) {\displaystyle \theta =\arccos({\boldsymbol {\hat {a}}}}cdot {\boldsymbol {\hat {b}}})}

Ker je kosinus 90° enak nič, je točkovni produkt dveh pravokotnih vektorjev vedno enak nič. Poleg tega lahko dva vektorja štejemo za pravokotna, če in samo če je njun točkovni produkt enak nič in če imata oba neničelno dolžino. Ta lastnost omogoča preprosto metodo za preverjanje pogoja ortogonalnosti.

Včasih se te lastnosti uporabljajo tudi za opredelitev točkovnega produkta, zlasti v 2 in 3 razsežnostih; ta opredelitev je enakovredna zgornji. Pri višjih dimenzijah lahko formulo uporabimo za opredelitev pojma kota.

Geometrijske lastnosti temeljijo na tem, da je osnova ortonormalna, tj. sestavljena iz parno pravokotnih vektorjev z enotsko dolžino.

Skalarna projekcija

Če imata a in b dolžino ena (tj. sta vektorja enote), je njun točkovni produkt preprosto kosinus kota med njima.

Če je le b enotski vektor, potem je točkovni produkt a - b |a| cos(θ), tj. velikost projekcije a v smeri b, z minusom, če je smer nasprotna. To imenujemo skalarna projekcija a na b ali skalarna komponenta a v smeri b (glej sliko). Ta lastnost točkovnega produkta ima več uporabnih aplikacij (glej na primer naslednje poglavje).

Če niti a niti b nista enotski vektor, potem je na primer velikost projekcije a v smeri b enaka a - (b / |b|), saj je enotski vektor v smeri b enak b / |b|.

Vrtenje

Vrtenje ortonormalne osnove, v kateri je predstavljen vektor a, dobimo z množenjem a z matriko vrtenja R. To množenje matrik je le kompaktna predstavitev zaporedja točkovnih produktov.

Naj na primer

• B₁ = {x, y, z} in B₂ = {u, v, w} sta dve različni ortonormalni bazi istega prostora R³ , pri čemer B₂ dobimo tako, da B₁ samo zavrtimo,
• a₁ = (a_x , a_y , a_z ) predstavlja vektor a v smislu B₁ ,
• a₂ = (a_u , a_v , a_w ) predstavljajo isti vektor v smislu zasukane osnove B₂ ,
• u₁ , v₁ , w₁ so zasukani bazni vektorji u, v, w, predstavljeni v obliki B₁ .

Nato se vrtenje iz B₁ v B₂ izvede na naslednji način:

a 2 = R a 1 = [ u x u y u z v x v y v z w x w y w z ] [ a x a y a z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {Ra}}_{1}={\begin{bmatrix}u_{x}&u_{y}&u_{z}\\v_{x}&v_{y}&v_{z}\\w_{x}&w_{y}&w_{z}\end{bmatrix}}{\begin{bmatrix}a_{x}\\a_{y}\\a_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}\\{\mathbf {w}}_{1}\cdot {\mathbf {a}}}_{1}\end{bmatrix}}}={\begin{bmatrix}a_{u}\a_{v}\a_{w}\end{bmatrix}}. }

Opazite, da je matrika rotacije R sestavljena tako, da se kot vrstice uporabijo vrteči se osnovni vektorji u₁ , v₁ , w₁ , ti vektorji pa so enotski vektorji. Po definiciji je Ra₁ sestavljen iz zaporedja točkovnih produktov med vsako od treh vrstic R in vektorjem a₁ . Vsak od teh točkovnih produktov določa skalarno komponento a v smeri vrtenega baznega vektorja (glej prejšnje poglavje).

Če je₁ vrstični in ne stolpčni vektor, potem mora R vsebovati vrteče se bazne vektorje v svojih stolpcih in mora naknadno pomnožiti₁ :

a 2 = a 1 R = [ a x a y a z ] [ u x v x w x u y v y w y u z v z w z ] = [ u 1 ⋅ a 1 v 1 ⋅ a 1 w 1 ⋅ a 1 ] = [ a u a v a w ] . {\displaystyle {\mathbf {a}}_{2}={\mathbf {a}}_{1}{\mathbf {R}}={\begin{bmatrix}a_{x}&a_{y}&a_{z}\end{bmatrix}}{\begin{bmatrix}u_{x}&v_{x}&w_{x}\\u_{y}&v_{y}&w_{y}\\u_{z}&v_{z}&w_{z}\end{bmatrix}}={\begin{bmatrix}{\mathbf {u}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {v}}_{1}\cdot {\mathbf {a}}_{1}&{\mathbf {w}}_{1}\cdot {\mathbf {a}}_{1}\end{bmatrix}}={\begin{bmatrix}a_{u}&a_{v}&a_{w}\end{bmatrix}}. }

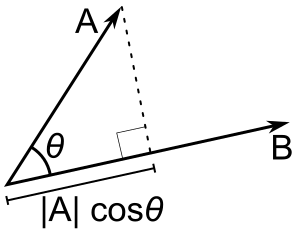
A - B = |A| |B| cos(θ). |A| cos(θ) je skalarna projekcija A na B.

Fizika

V fiziki je magnituda skalar v fizikalnem smislu, tj. fizikalna količina, neodvisna od koordinatnega sistema, izražena kot produkt številske vrednosti in fizikalne enote, in ne le kot število. Tudi točkovni produkt je skalar v tem smislu, podan s formulo, neodvisen od koordinatnega sistema. Primer:

• Mehansko delo je točkovni produkt vektorjev sile in premika.
• Magnetni tok je točkovni produkt magnetnega polja in površinskih vektorjev.
• Volumski pretok je točkovni produkt vektorjev hitrosti tekočine in površine.

Lastnosti

Če so a, b in c realni vektorji, r pa skalar, veljajo naslednje lastnosti.

Pika produkt je komutativen:

a ⋅ b = b ⋅ a . {\displaystyle \mathbf {a} \cdot \mathbf {b} =\mathbf {b} \cdot \mathbf {a} . }

Potečni produkt je distributivni v primerjavi z vektorskim seštevanjem:

a ⋅ ( b + c ) = a ⋅ b + a ⋅ c . {\displaystyle \mathbf {a} \cdot (\mathbf {b} +\mathbf {c} )=\mathbf {a} \cdot \mathbf {b} +\mathbf {a} \cdot \mathbf {c} . }

Potečni produkt je bilinearen:

a ⋅ ( r b + c ) = r ( a ⋅ b ) + ( a ⋅ c ) . {\displaystyle \mathbf {a} \cdot (r\mathbf {b} +\mathbf {c} )=r(\mathbf {a} \cdot \mathbf {b} )+(\mathbf {a} \cdot \mathbf {c} ). }

Ko se pomnoži s skalarno vrednostjo, je točkovni produkt enak:

( c 1 a ) ⋅ ( c 2 b ) = ( c 1 c 2 ) ( a ⋅ b ) {\displaystyle (c_{1}\mathbf {a} )\cdot (c_{2}\mathbf {b} )=(c_{1}c_{2})(\mathbf {a} \cdot \mathbf {b} )}

(zadnji dve lastnosti sledita iz prvih dveh).

Dva neničelna vektorja a in b sta pravokotna, če in samo če a - b = 0.

V nasprotju z množenjem navadnih števil, kjer je ab = ac, potem je b vedno enak c, razen če je a enak nič, se točkovni produkt ne ravna po zakonu o izničenju:

Če je a - b = a - c in a ≠ 0, potem lahko zapišemo: a - (b - c) = 0 po distributivnem zakonu; zgornji rezultat pravi, da to samo pomeni, da je a pravokoten na (b - c), kar še vedno omogoča, da je (b - c) ≠ 0 in zato b ≠ c.

Če je osnova ortonormalna, je točkovni produkt invarianten pri izometričnih spremembah osnove: rotacijah, refleksijah in kombinacijah, pri čemer je izhodišče fiksno. Zgoraj omenjena geometrijska interpretacija temelji na tej lastnosti. Z drugimi besedami, za ortonormalen prostor s poljubnim številom dimenzij je točkovni produkt invarianten pri transformaciji koordinat, ki temelji na ortogonalni matriki. To ustreza naslednjim dvema pogojema:

• Nova osnova je spet ortonomna (tj. je ortonomna, izražena v stari bazi).
• Novi bazni vektorji imajo enako dolžino kot stari (tj. enoto dolžine glede na staro bazo).

Če sta a in b funkciji, potem je derivativ a - b enak a' - b + a - b'

Razširitev trojnega izdelka

To je zelo uporabna identiteta (znana tudi kot Lagrangeova formula), ki vključuje točkovni in navzkrižni produkt. Zapišemo jo kot

a × ( b × c ) = b ( a ⋅ c ) - c ( a ⋅ b ) {\displaystyle \mathbf {a} \times (\mathbf {b} \times \mathbf {c} )=\mathbf {b} (\mathbf {a} \cdot \mathbf {c} )-\mathbf {c} (\mathbf {a} \cdot \mathbf {b} )}

ki si ga je lažje zapomniti kot "BAC minus CAB", pri čemer ne smemo pozabiti, kateri vektorji so postavljeni skupaj. Ta formula se pogosto uporablja za poenostavitev vektorskih izračunov v fiziki.

Dokaz geometrijske interpretacije

Razmislite o elementu R ⁿ

v = v 1 e ^ 1 + v 2 e ^ 2 + ... + v n e ^ n . {\displaystyle \mathbf {v} =v_{1}\mathbf {\hat {e}} _{1}+v_{2}\mathbf {\hat {e}} _{2}+...+v_{n}\mathbf {\hat {e}} _{n}.\,}

Ob večkratni uporabi Pitagorovega izreka dobimo za njegovo dolžino |v|

| v | 2 = v 1 2 + v 2 2 + ... + v n 2 . {\displaystyle |\mathbf {v} |^{2}=v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2}.\,}

Vendar je to enako kot

v ⋅ v = v 1 2 + v 2 2 + ... + v n 2 , {\displaystyle \mathbf {v} \cdot \mathbf {v} =v_{1}^{2}+v_{2}^{2}+...+v_{n}^{2},\,}

zato sklepamo, da dobimo s točkovnim produktom vektorja v s samim seboj kvadratno dolžino vektorja.

Lemma 1

v ⋅ v = | v | 2 . {\displaystyle \mathbf {v} \cdot \mathbf {v} =|\mathbf {v} |^{2}.\,}

Sedaj upoštevajmo dva vektorja a in b, ki izhajata iz izhodišča in sta med seboj ločena za kot θ. Tretji vektor c lahko definiramo kot

c = d e f a - b . {\displaystyle \mathbf {c} \ {\stackrel {\mathrm {def} }{=}}\\ \mathbf {a} -\mathbf {b} .\,}

in tako dobimo trikotnik s stranicami a, b in c. V skladu z zakonom kosinusov imamo

| c | 2 = | a | 2 + | b | 2 - 2 | a | | b | cos θ . {\displaystyle |\mathbf {c} |^{2}=|\mathbf {a} |^{2}+|\mathbf {b} |^{2}-2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Če v skladu z Lemmo 1 zamenjamo točkovne produkte za kvadratne dolžine, dobimo

c ⋅ c = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,} (1)

Ker pa je c ≡ a - b, imamo tudi

c ⋅ c = ( a - b ) ⋅ ( a - b ) {\displaystyle \mathbf {c} \cdot \mathbf {c} =(\mathbf {a} -\mathbf {b} )\cdot (\mathbf {a} -\mathbf {b} )\,} ,

ki se v skladu z distributivnim zakonom razširi na

c ⋅ c = a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) . {\displaystyle \mathbf {c} \cdot \mathbf {c} =\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} ).\,} (2)

Z združitvijo dveh enačb c - c, (1) in (2), dobimo

a ⋅ a + b ⋅ b - 2 ( a ⋅ b ) = a ⋅ a + b ⋅ b - 2 | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2(\mathbf {a} \cdot \mathbf {b} )=\mathbf {a} \cdot \mathbf {a} +\mathbf {b} \cdot \mathbf {b} -2|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Če od obeh strani odštejemo a - a + b - b in delimo z -2, dobimo

a ⋅ b = | a | | b | cos θ . {\displaystyle \mathbf {a} \cdot \mathbf {b} =|\mathbf {a} ||\mathbf {b} |\cos \theta .\,}

Q.E.D.

Posplošitev

Notranji produkt posplošuje točkovni produkt na abstraktne vektorske prostore in je običajno označen z ⟨ a , b ⟩ {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle } . Zaradi geometrijske interpretacije točkovnega produkta je norma ||a|| vektorja a v takem prostoru notranjega produkta opredeljena kot

‖ a ‖ = ⟨ a , a ⟩ {\displaystyle \|\mathbf {a} \|={\sqrt {\langle \mathbf {a} \,,\mathbf {a} \rangle }}}

tako da posplošuje dolžino, kot θ med dvema vektorjema a in b pa z

cos θ = ⟨ a , b ⟩ ‖ a ‖ ‖ b ‖ . {\displaystyle \cos {\theta }={\frac {\langle \mathbf {a} \,,\mathbf {b} \rangle }{\|\mathbf {a} \|\,\|\mathbf {b} \|}}. }

Dva vektorja sta pravokotna, če je njun notranji produkt enak nič.

⟨ a , b ⟩ = 0. {\displaystyle \langle \mathbf {a} \,,\mathbf {b} \rangle =0.}

Za vektorje s kompleksnimi vpisi bi uporaba dane definicije točkovnega produkta privedla do povsem drugačnih geometrijskih lastnosti. Na primer, točkovni produkt vektorja s samim seboj je lahko poljubno kompleksno število in je lahko enak nič, ne da bi bil vektor ničelni vektor; to pa bi imelo hude posledice za pojme, kot sta dolžina in kot. Številne geometrijske lastnosti je mogoče rešiti na račun odpovedi simetričnim in bilinearnim lastnostim skalarnega produkta z alternativno opredelitvijo

a ⋅ b = ∑ a i b i ž {\displaystyle \mathbf {a} \cdot \mathbf {b} =\sum {a_{i}{\overline {b_{i}}}}}

kjer je b _ikompleksni konjugat b_i . Potem je skalarni produkt vsakega vektorja s samim seboj nenegativno realno število in je neničelno, razen za ničelni vektor. Vendar ta skalarni produkt ni linearen v b (temveč konjugiran linearen) in skalarni produkt tudi ni simetričen, saj

a ⋅ b = b ⋅ a ¯ {\displaystyle \mathbf {a} \cdot \mathbf {b} ={\overline {\mathbf {b} \cdot \mathbf {a} }}} .

Ta vrsta skalarnega produkta je kljub temu zelo uporabna in vodi do pojmov hermitske oblike in splošnih notranjih produktnih prostorov.

Frobeniusov notranji produkt posplošuje točkovni produkt na matrike. Definiran je kot vsota produktov ustreznih komponent dveh matrik enake velikosti.

Posplošitev na tenzorje

Točkovni produkt med tenzorjem reda n in tenzorjem reda m je tenzor reda n+m-2. Točkovni produkt dobimo tako, da pomnožimo in seštejemo en indeks v obeh tenzorjih. Če A {\displaystyle \mathbf {A} } in B {\displaystyle \mathbf {B} } sta dva tenzorja s predstavo elementov A i j ... k ℓ ... {\displaystyle A_{ij\dots }^{k\ell \dots }} in B m n ... p ... i {\displaystyle B_{mn\dots }^{p{\dots }i}} elementi točkovnega produkta A ⋅ B {\displaystyle \mathbf {A} \cdot \mathbf {B} } so podani z

A i j ... k ℓ ... B m n ... p ... i = ∑ i = 1 n A i j ... k ℓ ... B m n ... p ... i {\displaystyle A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}=\sum _{i=1}^{n}A_{ij\dots }^{k\ell \dots }B_{mn\dots }^{p{\dots }i}}

Ta definicija se seveda zmanjša na standardni vektorski točkovni produkt, kadar se uporablja za vektorje, in na matrično množenje, kadar se uporablja za matrike.

Občasno se za predstavitev množenja in seštevanja dveh indeksov uporablja dvojni točkovni produkt. Dvojni točkovni produkt med dvema tenzorjema 2. reda je skalar.

Sorodne strani

• Cauchy-Schwarzova neenakost
• Navzkrižni izdelek
• Množenje matrik
• Fizika